Have you ever wondered, “How can we predict global average temperature change when we don’t even know what the global average temperature is?”

Or maybe, “How can climate models produce any meaningful forecasts when they have such large errors in their component energy fluxes?” (This is the issue I’ve been debating with Dr. Pat Frank after publication of his Propagation of Error and the Reliability of Global Air Temperature Projections. )

I like using simple analogies to demonstrate basic concepts

Pots of Water on the Stove

A pot of water warming on a gas stove is useful for demonstrating basic concepts of energy gain and energy loss, which together determine temperature of the water in the pot.

If we view the pot of water as a simple analogy to the climate system, with a stove flame (solar input) heating the pots, we can see that two identical pots can have the same temperature, but with different rate of energy gain and loss, if (for example) we place a lid on one of the pots.

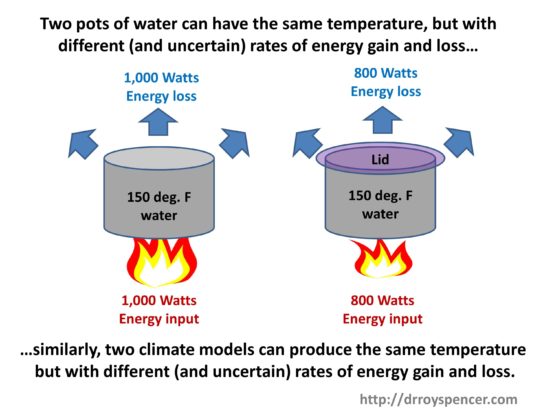
A lid reduces the warming water’s ability to cool, so the water temperature goes up (for the same rate of energy input) compared to if no lid was present. As a result, a lower flame is necessary to maintain the same water temperature as the pot without a lid. The lid is analogous to Earth’s greenhouse effect, which reduces the ability of the Earth’s surface to cool to outer space.

The two pots in the above cartoon are analogous to two climate models having different energy fluxes with known (and unknown) errors in them. The models can be adjusted so the various energy fluxes balance in the long term (over centuries) but still maintain a constant global average surface air temperature somewhere close to that observed. (The model behavior is also compared to many observed ocean and atmospheric variables. Surface air temperature is only one.)

Next, imagine that we had twenty pots with various amounts of coverage of the pots by the lids: from no coverage to complete coverage. This would be analogous to 20 climate models having various amounts of greenhouse effect (which depends mostly on high clouds [Frank’s longwave cloud forcing in his paper] and water vapor distributions). We can adjust the flame intensity until all pots read 150 deg. F. This is analogous to adjusting (say) low cloud amounts in the climate models, since low clouds have a strong cooling effect on the climate system by limiting solar heating of the surface.

Numerically Modeling the Pot of Water on the Stove

Now, let’s say we we build a time-dependent computer model of the stove-pot-lid system. It has equations for the energy input from the flame, and loss of energy from conduction, convection, radiation, and evaporation.

Clearly, we cannot model each component of the energy fluxes exactly, because (1) we can’t even measure them exactly, and (2) even if we could measure them exactly, we cannot exactly model the relevant physical processes. Modeling of real-world systems always involves approximations. We don’t know exactly how much energy is being transferred from the flame to the pot. We don’t know exactly how fast the pot is losing energy to its surroundings from conduction, radiation, and evaporation of water.

But we do know that if we can get a constant water temperature, that those rates of energy gain and energy loss are equal, even though we don’t know their values.

Thus, we can either make ad-hoc bias adjustments to the various energy fluxes to get as close to the desired water temperature as we want (this is what climate models used to do many years ago); or, we can make more physically-based adjustments because every computation of physical processes that affect energy transfer has uncertainties, say, a coefficient of turbulent heat loss to the air from the pot. This is what model climate models do today for adjustments.

If we then take the resulting “pot model” (ha-ha) that produces a water temperature of 150 deg. F as it is integrated over time, with all of its uncertain physical approximations or ad-hoc energy flux corrections, and run it with a little more coverage of the pot by the lid, we know the modeled water temperature will increase. That part of the physics is still in the model.

This is why climate models can have uncertain energy fluxes, with substantial known (or even unknown) errors in their energy flux components, and still be run with increasing CO2 to produce warming, even though that CO2 effect might be small compared to the errors. The errors have been adjusted so they sum to zero in the long-term average.

This directly contradicts the succinctly-stated main conclusion of Frank’s paper:

“LWCF [longwave cloud forcing] calibration error is +/- 144 x larger than the annual average increase in GHG forcing. This fact alone makes any possible global effect of anthropogenic CO2 emissions invisible to present climate models.”

I’m not saying this is ideal, or even a defense of climate model projections. Climate models should ideally produce results entirely based upon physical first principles. For the same forcing scenario (e.g. a doubling of atmospheric CO2) twenty different models should all produce about the same amount of future surface warming. They don’t.

Instead, after 30 years and billions of dollars of research they still produce from 1.5 to 4.5 deg. C of warming in response to doubling of atmospheric CO2.

The Big Question

The big question is, “How much will the climate system warm in response to increasing CO2?” The answer depends not so much upon uncertainties in the component energy fluxes in the climate system, as Frank claims, but upon how those energy fluxes change as the temperature changes.

And that’s what determines “climate sensitivity”.

This is why people like myself and Lindzen emphasize so-called “feedbacks” (which determine climate sensitivity) as the main source of uncertainty in global warming projections.