I keep getting requests to comment on the recent GRL paper by Lindzen and Choi (2009), who computed how satellite-measured net (solar + infrared) radiation in the tropics varied with surface temperature changes over the 15 year period of record of the Earth Radiation Budget Satellite (ERBS, 1985-1999).

The ERBS satellite carried the Earth Radiation Budget Experiment (ERBE) which provided our first decadal-time scale record of quasi-global changes in absorbed solar and emitted infrared energy. Such measurements are critical to our understanding of feedbacks in the climate system, and thus to any estimates of how the climate system responds to anthropogenic greenhouse gas emissions.

The authors showed that satellite-observed radiation loss by the Earth increased dramatically with warming, often in excess of 6 Watts per sq. meter per degree (6 W m^-2 K^-1). In stark contrast, all of the computerized climate models they examined did just the opposite, with the atmosphere trapping more radiation with warming rather than releasing more.

The implication of their results was clear: most if not all climate models that predict global warming are far too sensitive, and thus produce far too much warming and associated climate change in response to humanity’s carbon dioxide emissions.

A GOOD METHODOLOGY: FOCUS ON THE LARGEST TEMPERATURE CHANGES

One thing I liked about the authors’ analysis is that they examined only those time periods with the largest temperature changes – whether warming or cooling. There is a good reason why one can expect a more accurate estimate of feedback by just focusing on those large temperature changes, rather than blindly treating all time periods equally. The reason is that feedback is the radiation change RESULTING FROM a temperature change. If there is a radiation change, but no temperature change, then the radiation change obviously cannot be due to feedback. Instead, it would be from some internal variation in cloudiness not caused by feedback.

But it also turns out that a non-feedback radiation change causes a time-lagged temperature change which completely obscures the resulting feedback. In other words, it is not possible to measure the feedback in response to a radiatively induced temperature change that can not be accurately quantified (e.g., from chaotic cloud variations in the system). This is the subject of several of my previous blog postings, and is addressed in detail in our new JGR paper — now in review — entitled, “On the Diagnosis of Radiative Feedbacks in the Presence of Unknown Radiative Forcing”, by Spencer and Braswell).

WHAT DO THE AMIP CLIMATE MODEL RESULTS MEAN?

Now for my main concern. Lindzen and Choi examined the AMIP (Atmospheric Model Intercomparison Project) climate model runs, where the sea surface temperatures (SSTs) were specified, and the model atmosphere was then allowed to respond to the specified surface temperature changes. Energy is not conserved in such model experiments since any atmospheric radiative feedback which develops (e.g. a change in vapor or clouds) is not allowed to then feed-back upon the surface temperature, which is what happens in the real world.

Now, this seems like it might actually be a GOOD thing for estimating feedbacks, since (as just mentioned) most feedbacks are the atmospheric response to surface forcing, not the surface response to atmospheric forcing. But the results I have been getting from the fully coupled ocean-atmosphere (CMIP) model runs that the IPCC depends upon for their global warming predictions do NOT show what Lindzen and Choi found in the AMIP model runs. While the authors found decreases in radiation loss with short-term temperature increases, I find that the CMIP models exhibit an INCREASE in radiative loss with short term warming.

In fact, a radiation increase MUST exist for the climate system to be stable, at least in the long term. Even though some of the CMIP models produce a lot of global warming, all of them are still stable in this regard, with net increases in lost radiation with warming (NOTE: If analyzing the transient CMIP runs where CO2 is increased over long periods of time, one must first remove that radiative forcing in order to see the increase in radiative loss).

So, while I tend to agree with the Lindzen and Choi position that the real climate system is much less sensitive than the IPCC climate models suggest, it is not clear to me that their results actually demonstrate this.

ANOTHER VIEW OF THE ERBE DATA

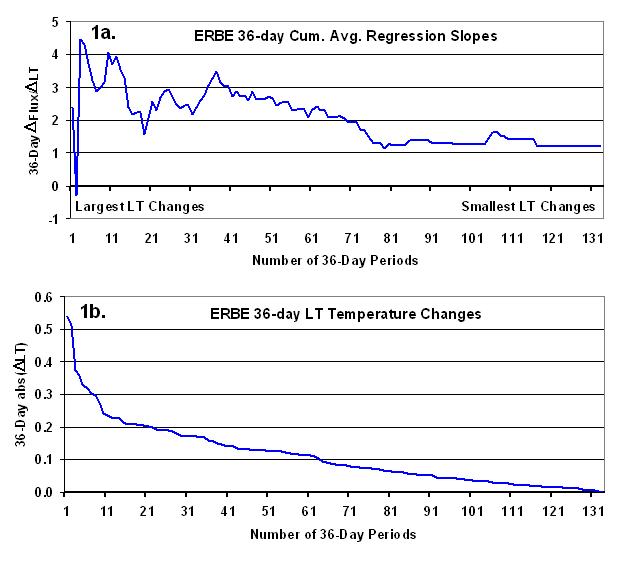
Since I have been doing similar computations with the CERES satellite data, I decided to do my own analysis of the re-calibrated ERBE data that Lindzen and Choi analyzed. Unfortunately, the ERBE data are rather dicey to analyze because the ERBE satellite orbit repeatedly drifted in and out of the day-night (diurnal) cycle. As a result, the ERBE Team advises that one should only analyze 36-day intervals (or some multiple of 36 days) for data over the deep tropics, while 72-day averages are necessary for the full latitudinal extent of the satellite data (60N to 60S latitude).

Lindzen and Choi instead did some multi-month averaging in an apparent effort to get around this ‘aliasing’ problem, but my analysis suggests that the only way around the problem it is to do just what the ERBE Team recommends: deal with 36 day averages (or even multiples of that) for the tropics; 72 day averages for the 60N to 60S latitude band. So it is not clear to me whether the multi-month averaging actually removed the aliased signal from the satellite data. I tried multi-month averaging, too, but got very noisy results.

Next, since they were dealing with multi-month averages, Lindzen and Choi could use available monthly sea surface temperature datasets. But I needed 36-day averages. So, since we have daily tropospheric temperatures from the MSU/AMSU data, I used our (UAH) lower tropospheric temperatures (LT) instead of surface temperatures. Unfortunately, this further complicates any direct comparisons that might be made between my computations (shown below) and those of Lindzen and Choi.

Finally, rather than picking specific periods where the temperature changes were particularly large, like Lindzen and Choi did, I computed results from ALL time periods, but then sorted the results from the largest temperature changes to the smallest. This allows me to compute and plot cumulative average regression slopes from the largest to the smallest temperature changes, so we can see how the diagnosed feedbacks vary as we add more time intervals with progressively weaker temperature changes.

RESULTS

For the 20N-20S latitude band (same as that analyzed by Lindzen and Choi), and at 36-day averaging time, the following figure shows the diagnosed feedback parameters (linear regression slopes) tend to be in the range of 2 to 4 W m^-2 K^-1, which is considerably smaller than what Lindzen and Choi found, which were often greater than 6 W m^-2 K^-1. As mentioned above, the corresponding climate model computations they made had the opposite sign, but as I have pointed out, the CMIP models do not, and the real climate system cannot have a net negative feedback parameter and still be stable.

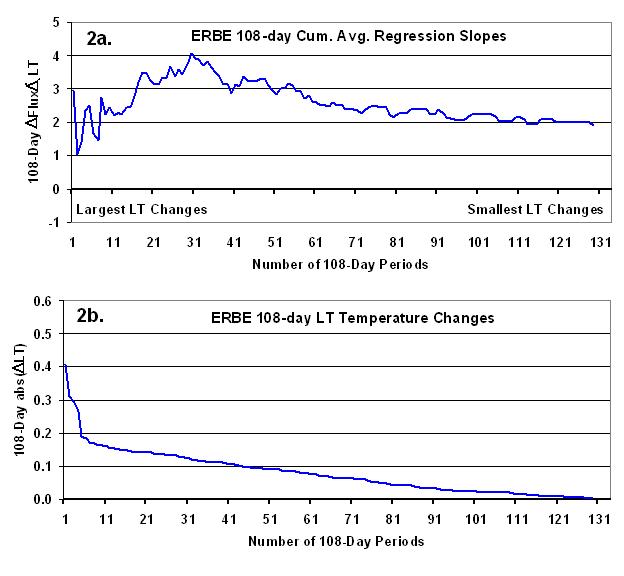
But since the Lindzen and Choi results were for changes on time scales longer than 36 days, next I computed similar statistics for 108-day averages. Once again we see feedback diagnoses in the range of 2 to 4 W m^-2 K^-1:

Finally, I extended the time averaging to 180 days (five 36-day periods), which is probably closest to the time averaging that Lindzen and Choi employed. But rather than getting closer to the higher feedback parameter values they found, the result is instead somewhat lower, around 2 W m^-2 K^-1.

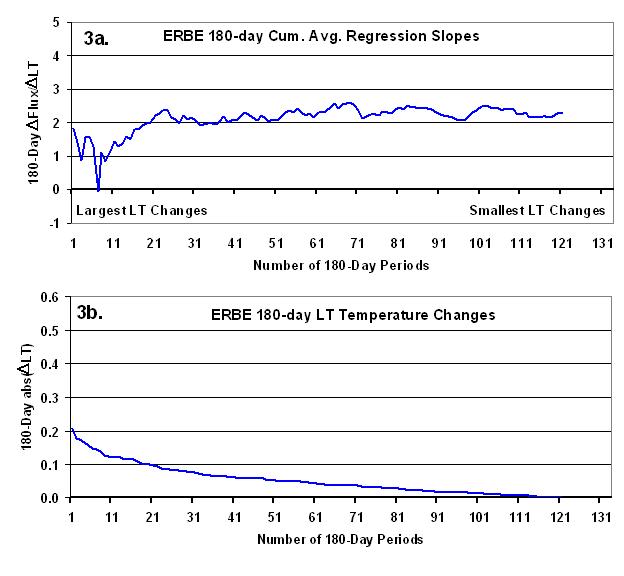
In all of these figures, running (not independent) averages were computed, always separated by the next average by 36 days.

By way of comparison, the IPCC CMIP (coupled ocean-atmosphere) models show long-term feedbacks generally in the range of 1 to 2 W m^-2 K^-1. So, my ERBE results are not that different from the models. BUT..it should be remembered that: (1) the satellite results here (and those of Lindzen and Choi) are for just the tropics, while the model feedbacks are for global averages; and (2) it has not yet been demonstrated that short-term feedbacks in the real climate system (or in the models) are substantially the same as the long-term feedbacks.

WHAT DOES ALL THIS MEAN?

It is not clear to me just what the Lindzen and Choi results mean in the context of long-term feedbacks (and thus climate sensitivity). I’ve been sitting on the above analysis for weeks since (1) I am not completely comfortable with their averaging of the satellite data, (2) I get such different results for feedback parameters than they got; and (3) it is not clear whether their analysis of AMIP model output really does relate to feedbacks in those models, especially since my analysis (as yet unpublished) of the more realistic CMIP models gives very different results.

Of course, since the above analysis is not peer-reviewed and published, it might be worth no more than what you paid for it. But I predict that Lindzen and Choi will eventually be challenged by other researchers who will do their own analysis of the ERBE data, possibly like that I have outlined above, and then publish conclusions that are quite divergent from the authors’ conclusions.

In any event, I don’t think the question of exactly what feedbacks are exhibited by the ERBE satellite is anywhere close to being settled.