Over the years I have gone along with the crowd and derided the term “greenhouse effect” as a poor analogy between the atmosphere’s ability to keep the Earth’s surfce warmer than it would be without IR-absorbing (and thus IR-emitting) gases, versus a greenhouse in which plants are grown.
Over the years I have gone along with the crowd and derided the term “greenhouse effect” as a poor analogy between the atmosphere’s ability to keep the Earth’s surfce warmer than it would be without IR-absorbing (and thus IR-emitting) gases, versus a greenhouse in which plants are grown.
But the more I think about it, the more I realize that “greenhouse effect” is a pretty accurate term.
The main objection has been that the warmth within a real greenhouse is primarily due to the roof’s ability to keep warm air from escaping, thus inhibiting convective heat loss. While that is true, it is also true of the atmospheric greenhouse effect.
Remember,
1) the roof of the greenhouse is also an IR absorber and emitter, like water vapor and CO2 do in the free atmosphere, and
2) the atmospheric greenhouse effect is only fully realized in the absence of convective heat loss.
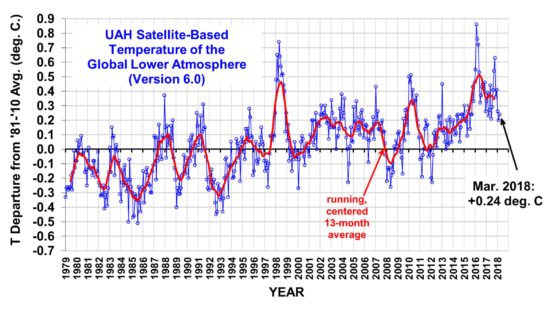
Let’s start with that second point. As originally calculated by Manabe and Strickler (1964, see slide #10 here), the greenhouse effect does not explain the average surface temperature being 288 K (observed) rather than 255K (the effective radiating temperature of the Earth absent an atmosphere). Instead it is actually much more powerful than that, and would raise the temperature to an estimated 343 K (close to 160 deg. F.) It is convective heat loss generated by an unstable lapse rate caused by the greenhouse effect that reduces the temperature to the observed value.
This is the actual “greenhouse effect” on Earth’s average surface temperature: not the oft-quoted 33 deg. C, but more like 88 deg. C of warming. (We can quibble about the calculations of surface temperature with and without greenhouse gases because they make unrealistic assumptions about clouds and water vapor.)
The point is, the atmospheric greenouse effect is radiative only, and does not include the cooling effects of convective heat transport away from the Earth’s surface.
Kind of like in a real greenhouse.
So, this actually is what happens in a real greenhouse:
1) sunlight warms the interior
2) infrared radiation absorbed and emitted by the roof reduces radiative energy loss by the air and surfaces within the greenhouse
3) convective heat loss is minimized (although it is generated on the outside surface of the roof, thus keeping the interior cooler than if there was no convective heat loss at all)
So, all things considered, I think we need to embrace the “greenhouse effect” concept. Plants like it so much, we artificially enhance Nature’s greenhouse effect (which existed before greenhouses were invented) for their benefit.
Next, let’s pump some extra CO2 in there to help the plants even more.


 Home/Blog
Home/Blog