A potential new poster child for global warming ignores the lack of trend in major hurricane landfalls in the Carolinas.

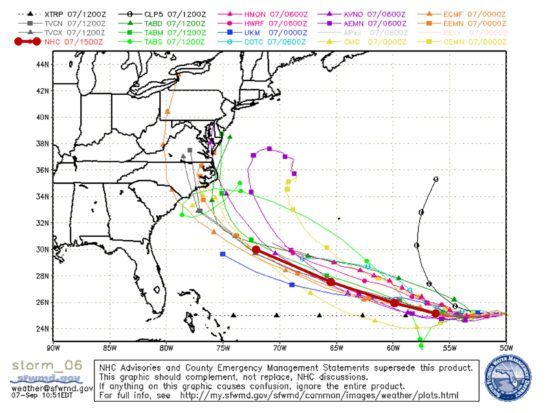
GOES-East image of rapidly-strengthening Hurricane Florence, forecast to arrive on the coast of the Carolinas as a Cat 4 storm on Thursday night, Sept. 13, 2018.
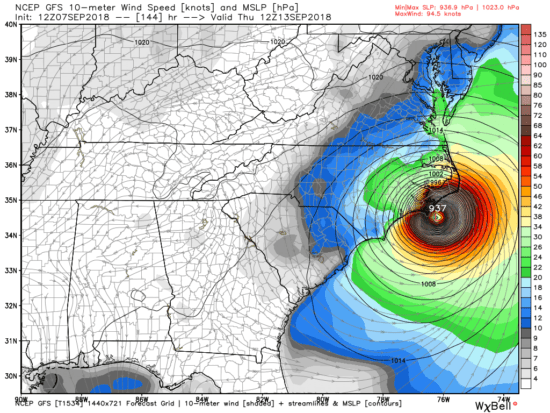
Although it is still 3-4 days away, rapidly strengthening Hurricane Florence is increasing the threat of a major hurricane landfall somewhere within 120 miles or so of Wilmington, NC. If it reaches that area as a Cat 4 storm, the damage produced will be extensive, likely amounting to tens of billions of dollars.
By coincidence, the hurricane disaster (if it unfolds) will occur during this year’s Global Climate Action Summit (Sept. 12-14) in San Francisco, possibly the most star-studded climate alarmist extravaganza in existence, with climate experts such as Al Gore, Alec Baldwin, Andrea Mitchell, Catherine McKenna, Dave Matthews, Jane Goodall, John Kerry, and Tom Steyer.
As we all know, these are people who lead by example in their efforts to reduce their so-called carbon footprints.

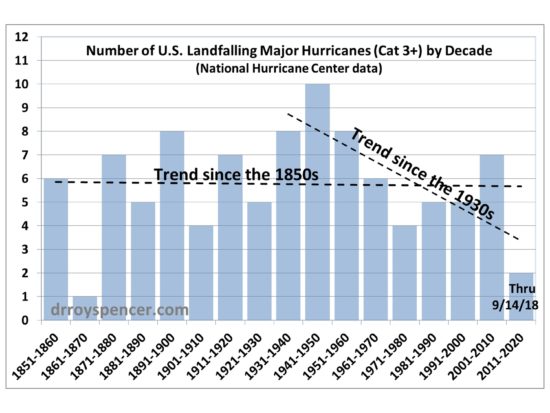
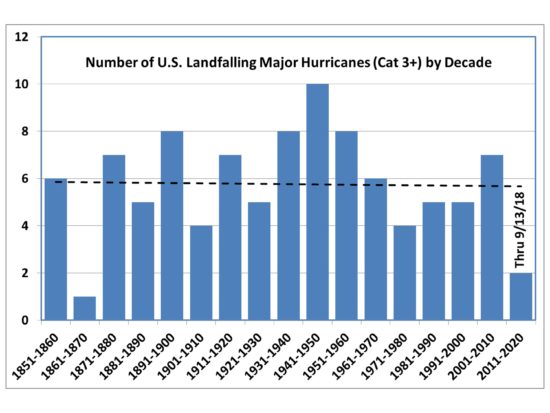
Attendees of the conference are almost guaranteed to point to Florence as an example of what we can expect more of with global warming. But it’s curious how there hasn’t been a statistically significant increase in major hurricane strikes in the Carolinas (based upon NHC data), even assuming Florence hits as a Cat3+:
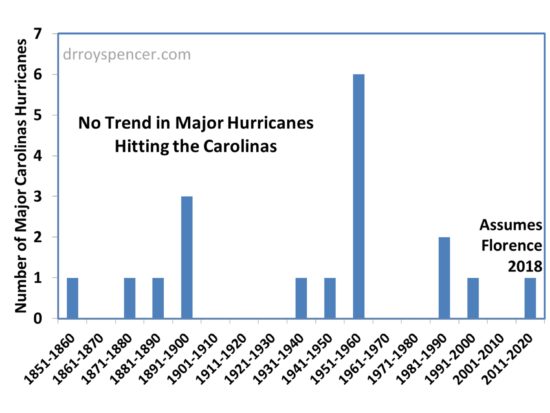
(The same is true in Florida.)
The 1950s was the stand-out decade for major hurricane strikes in the Carolinas, with Hurricane Hazel in 1954 doing major damage, even as far north as Toronto. Hazel’s destruction of Myrtle Beach, SC led to a massive rebuilding effort that transformed that community forever.
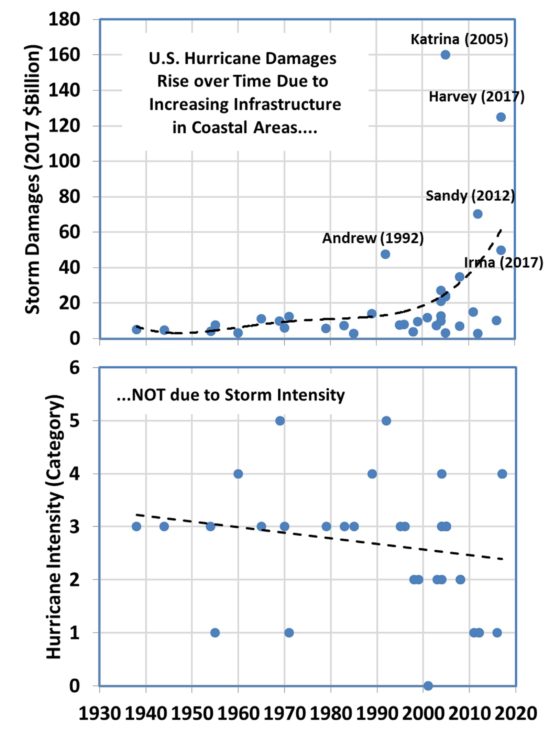
For sure, there has been an increase in hurricane damages over time, as infrastructure along the U.S. Gulf and Atlantic coasts has increased dramatically. There is simply more stuff for Mother Nature to destroy. But I doubt that the luminaries attending the Global Climate Action Summit this week can understand that increasing damages would occur even without any climate change.
Major hurricanes are business as usual for nature, just uncommon.
For now, let’s hope Florence weakens or stays offshore. But as the above chart shows, the Carolinas should not be surprised if a disaster occurs, at least based upon the history of major hurricane strikes.

 Home/Blog
Home/Blog