After watching the Oroville Dam crisis evolve over the last several days, and reading various experts’ opinions about what might be going on both with both the facility itself and behind the scenes decision-making, I thought it might be time to step back and discuss where we are at, and where we might be going.
The Dam Spillway Situation
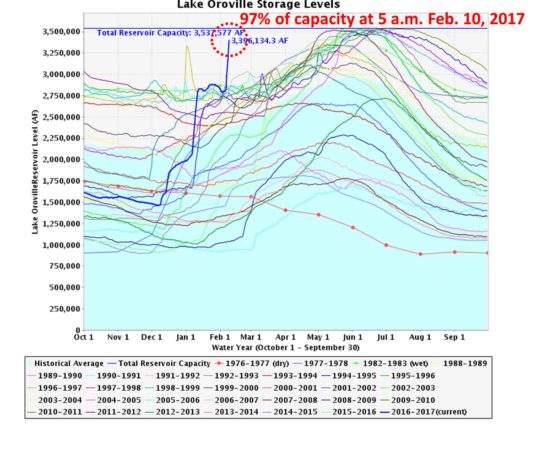
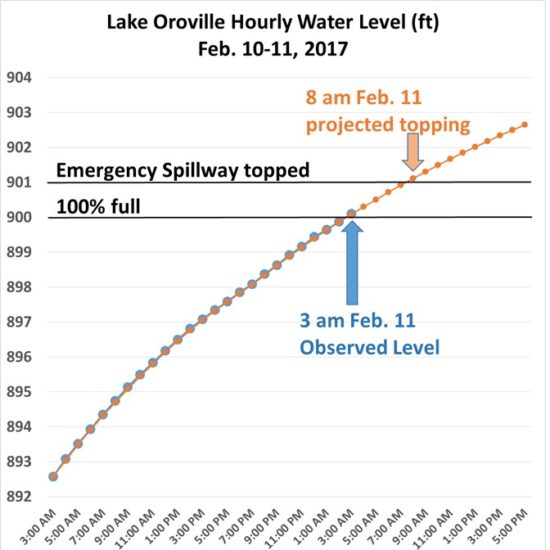
First of all, the immediate crisis has passed. At this writing (4 a.m. PST Tuesday), the lake level has been lowered to 11 feet below the emergency spillway, and is dropping at a rate of about 8 feet per day. The goal is to get it to about 50 feet below the top of the concrete weir of the emergency spillway, which was topped by 1.5 feet at the peak of the crisis.
That’s the good news.
The bad news is that in order to achieve this, the flow through the main concrete-lined spillway, which has been heavily damaged, has had to be increased to 100,000 cubic feet per second (CFS), creating a spectacular waterfall over the lip of the remaining portion of the concrete flume:
More on that later.
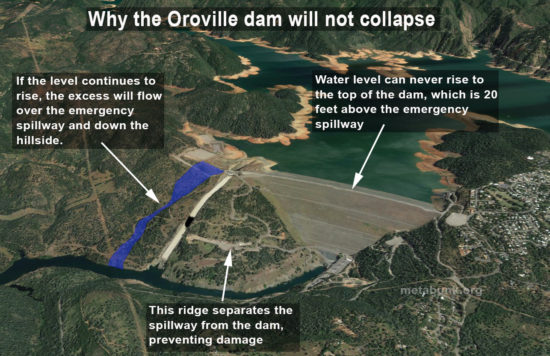
The other bad news is that the relatively brief use of the emergency spillway led to a lot more erosion into the rock below the concrete weir than engineers expected. This rapid erosion is why evacuations were suddenly ordered, since there were fears that it would backcut to the concrete weir, which was at risk of collapse:
If that happened, a 30 ft. wall of water would cascade downstream. At least two large gouges are currently being patched with sacks of rock and some concrete. The emergency spillway was supposedly designed to handle 350,000 CFS, but it only took a day at 10,000 CFS to cause the damage, leading up to an official warning that the spillway could collapse within an hour and the mandatory evacuation order. (The main earthfill portion of the dam is in no danger, since the emergency spillway, 20 ft. below the level of the main dam, would keep the main dam from ever being topped).
My (admittedly non-expert) view of the situation is that the emergency spillway is of lesser concern at this point. Rains will return Wednesday night beginning a 7-day wet period during which 5 to 12 inches of water-equivalent precipitation will fall on the watershed:
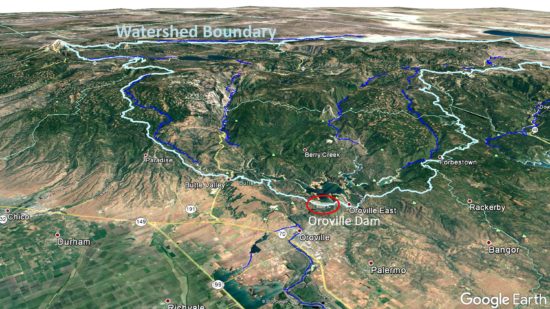
Google Earth view of the watershed feeding Oroville Lake. Much of this area is above 4,500-5,000 ft. elevation, where winter precipitation usually falls as snow.
That might sound bad, but the good news is that most of that precipitation will fall as snow, except over the lake itself, in contrast to earlier warm rain events that led to the current crisis.
Despite the new precipitation, I suspect that they will be able to keep the lake level to around 850-860 feet or so, which is 40-50 feet below full-pool. It might briefly rise by 10-20 feet if the rain is exceptionally heavy. The main danger to Northern California dams is heavy rain events; spring snow melt typically occurs more slowly and is easier to handle by adjusting outflow from reservoirs.
I further suspect that concern will be shifted to the main spillway, the continuing heavy use of which is absolutely required in order to keep the lake level low enough to allow repairs to the emergency spillway, as long as there is significant runoff into the lake.

Close-up of damage to main spillway on Feb. 7; the concrete wall in the foreground has since been destroyed with considerable erosion of the adjacent hillside (SacBee photo).
The hydro plant generators have been shut down from debris, and they would have only allowed an additional 16,000 CFS outflow anyway. The diversion tunnels were damaged years ago and are unusable.
So, the damaged main spillway is essentially the only way that the reservoir can shed substantial volumes of water as rains occur, and as spring snow melt begins.
I predict that they will shut the main spillway down soon to see how fast the damage is eroding uphill. If I had to guess, I’d say that shutdown might actually happen today…a three hour shutdown will only reduce the lake level fall by 1 foot. They need to assess the situation, because…
A PR Disaster is Rapidly Approaching
From watching the daily press briefings, I think that the experts and emergency officials have been less than forthcoming on details. As dam expert Scott Cahill wrote yesterday, the public has been treated a little like children so far. Reporters’ questions have gone unanswered, and the experts opinions have careened between “no danger” and “imminent failure” in less than 24 hours. (Update: Scott Cahill has a new essay today about how no one is ever accountable anymore in disaster situations…it’s all review panels and committees….the buck is passed from person to person until no one knows who has the buck.)
This is NOT the way for “experts” to engender confidence in the public.
Of particular concern is the estimated 185,000 residents who have evacuated to higher ground, and are anxious to return to their homes. We live in an age where we want results now, and the longer these people have to wait with only general information being provided, the more anger and frustration will grow. Reporters are going to cover this frustration, with face-to-face interviews, and officials had better get ahead of the impending PR disaster while they can.
When will people be allowed home? I can only speculate. If emergency officials are being very cautious they might wait until the coming wet weather period has passed, which would be at least 10 days to make sure the lake does not rise too much, and until after they have verified the concrete flume of the main spillway isn’t eroding uphill very much.
Or, they could let people return at any time, warning them to keep alert for a possible future evacuation with little notice. I really dont know. If I had to guess, I’d say they will go the cautious route. But if they were to inspect the main spillway today and see only minor additional erosion uphill from where it previously was, maybe they will let people come home very soon.
No matter what happens in the coming days and weeks, Oroville Dam will remain an issue for months — maybe even years — to come. Repairs will be expensive and lengthy. And there will be second-guessing of decisions made, including the 12-year old report by experts that the emergency spillway was just fine as-is.
(A detailed chronological discussion of the Oroville issues by mainly geologists, along with some amazing photos, can be followed here.)
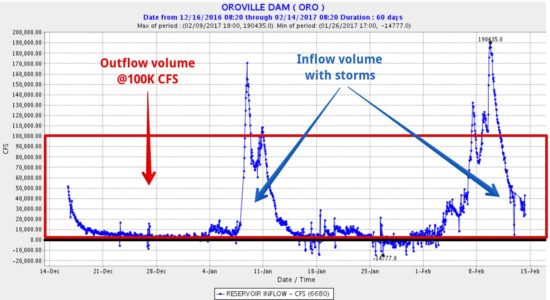
UPDATE: Mick West, Sacramento, provided this graphic which shows the volume of water that can be output from Lake Oroville at 100,000 CFS flow through the main spillway (area of the red box), versus what has flowed into the lake from precipitation in the last couple months (area under the blue curve). It suggests that the lake can probably be kept from completely filling again if 100,000 CFS outflow is maintained, with only temporary rises in lake level after heavy rain events:
Drone video of emergency spillway damage from evening of Feb. 13, 2017 (CA DWR).

 Home/Blog
Home/Blog