UPDATE #1 (12:30 p.m. CST, March 3): Appended new discussion & plots showing importance of how low-population density stations are handled.

UPDATE #2 (9:10 a.m. CST, March 4): Clarifications on methodology and answers to questions.

ABSTRACT
Global hourly surface temperature observations and 1 km resolution population density data for the year 2000 are used together to quantify the average urban heat island (UHI) effect. While the rate of warming with population increase is the greatest at the lowest population densities, some warming continues with population increases even for densely populated cities. Statistics like those presented here could be used to correct the surface temperature record for spurious warming caused by the UHI effect, providing better estimates of temperature trends.

METHOD
Using NOAA’s International Surface Hourly (ISH) weather data from around the world during 2000, I computed daily, monthly, and then 1-year average temperatures for each weather station. For a station to be used, a daily average temperature computation required the 4 synoptic temperature observations at 00, 06, 12, and 18 UTC; a monthly average required at least 20 good days per month; and a yearly average required all 12 months.

For each of those weather station locations I also stored the average population density from the 1 km gridded global population density data archived at the Socioeconomic Data and Applications Center (SEDAC).

All station pairs within 150 km of each other had their 1-year average difference in temperature related to their difference in population. Averaging of these station pairs’ results was done in 10 population bins each for Station1 and Station2, with bin boundaries at 0, 20, 50, 100, 200, 400, 800, 1600, 3200, 6400, and 50000 persons per sq. km.

Because some stations are located next to large water bodies, I used an old USAF 1/6 deg lat/lon percent water coverage dataset to ensure that there was no more than a 20% difference in the percent water coverage between the two stations in each match-up. (I believe this water coverage dataset is no longer publicly available).

Elevation effects were estimated by regressing station pair temperature differences against station elevation differences, which yielded a cooling rate of 5.4 deg. C per km increase in station elevation. Then, all station temperatures were adjusted to sea level (0 km elevation) with this relationship.

After all screening, a total of 10,307 unique station pairs were accepted for analysis from 2000.

RESULTS & DISCUSSION
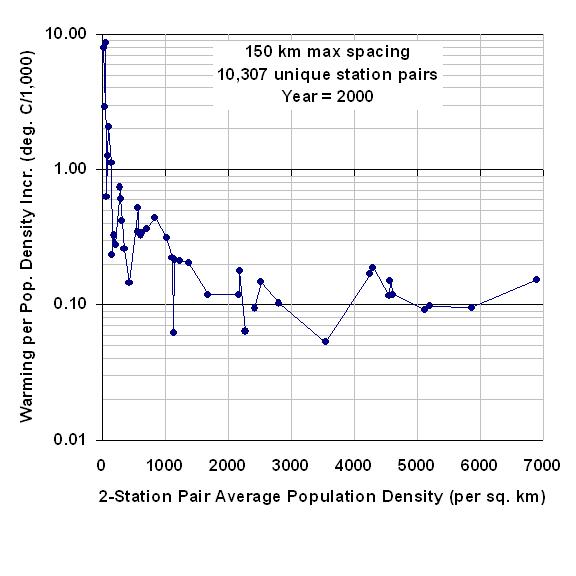
The following graph shows the average rate of warming with population density increase (vertical axis), as a function of the average populations of the station pairs. Each data point represents a population bin average for the intersection of a higher population station with its lower-population station mate.

Using the data in the above graph, we can now compute average cumulative warming from a population density of zero, the results of which are shown in the next graph. [Note that this step would be unnecessary if every populated station location had a zero-population station nearby. In that case, it would be much easier to compute the average warming associated with a population density increase.]

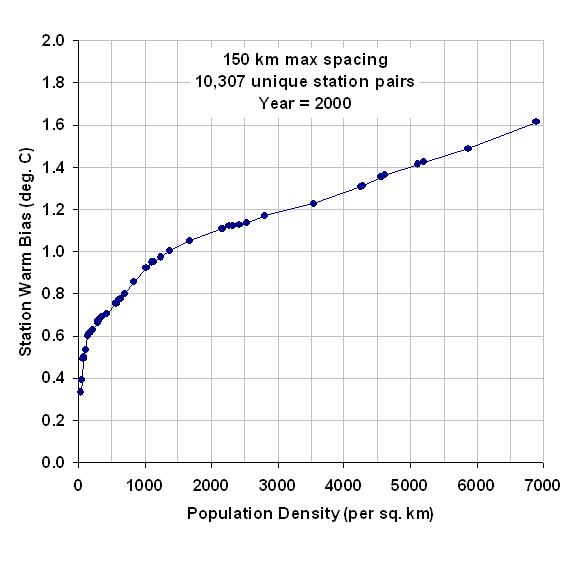
This graph shows that the most rapid rate of warming with population increase is at the lowest population densities. The non-linear relationship is not a new discovery, as it has been noted by previous researchers who found an approximate logarithmic dependence of warming on population.

Significantly, this means that monitoring long-term warming at more rural stations could have greater spurious warming than monitoring in the cities. For instance, a population increase from 0 to 20 people per sq. km gives a warming of +0.22 deg C, but for a densely populated location having 1,000 people per sq. km, it takes an additional 1,500 people (to 2,500 people per sq. km) to get the same 0.22 deg. C warming. (Of course, if one can find stations whose environment has not changed at all, that would be the preferred situation.)

Since this analysis used only 1 year of data, other years could be examined to see how robust the above relationship is. Also, since there are gridded population data for 1990, 2000, and 2010 (estimated), one could examine whether there is any indication of the temperature-population relationship changing over time.

This is the type of information which I can envision being used to adjust station temperatures throughout the historical record, even as stations come, go, and move. As mentioned above, the elevation adjustment for individual stations can be done fairly easily, and the population adjustments could then be done without having to inter-calibrate stations.

Such adjustments help to maximize the number of stations used in temperature trend analysis, rather than simply throwing the data out. Note that the philosophy here is not to provide the best adjustments for each station individually, but to do adjustments for spurious effects which, when averaged over all stations, will remove the effect when averaged over all stations. This ensures simplicity and reproducibility of the analysis.

UPDATE #1:
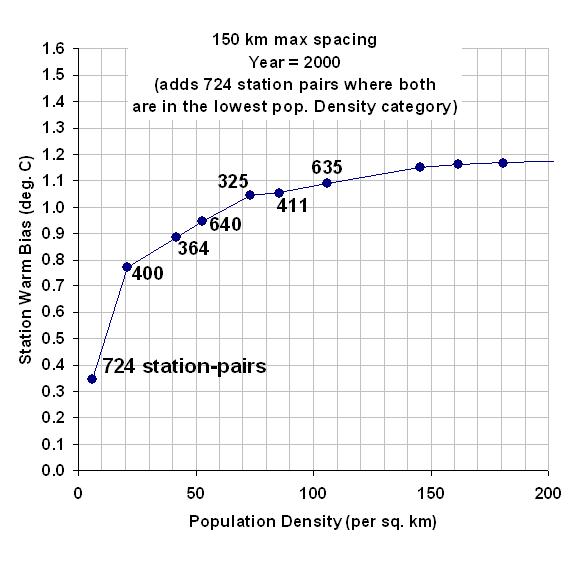
The above results are quite sensitive to how the stations with very low population densities are handled. I’ve recomputed the above results by adding a single data point representing 724 more station pairs where BOTH stations are within the lowest population density category: 0 to 20 people per sq. km. This increases the signal of warming at low population densities, from the previously mentioned +0.22 deg C warming from zero to 20 people per sq. km, to +0.77 deg. C of warming.

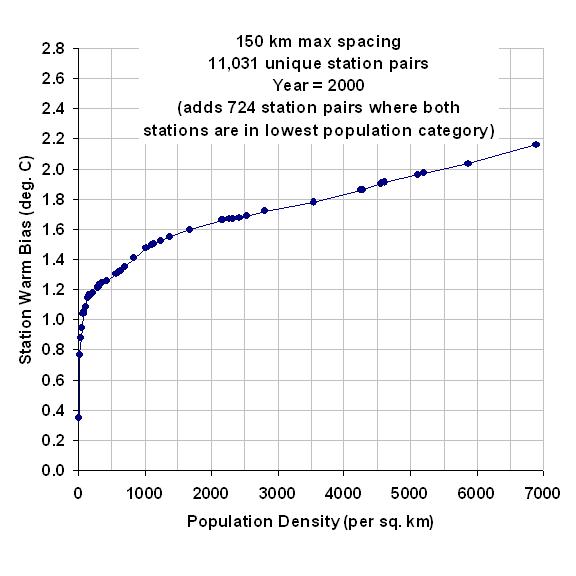
This is over a factor of 3 more warming from 0 to 20 persons per sq. km with the additional data. This is important because most weather observation sites have relatively low population densities: in my dataset, I find that one-half of all stations have population densities below 100 persons per sq. km. The following plot zooms in on the lower left corner of the previous plot so you can better see the warming at the lowest population densities.

Clearly, any UHI adjustments to past thermometer data will depend upon how the UHI effect is quantified at these very low population densities.

Also, since I didn’t mention it earlier, I should clarify that population density is just an accessible index that is presumed to be related to how much the environment around the thermometer site has been modified over time, by replacing vegetation with manmade structures. Population density is not expected to always be a good index of this modification — for instance, population densities at large airports can be expected to be low, but the surrounding runway surfaces and airplane traffic can be expected to cause considerable spurious warming, much more than would be expected for their population density.

UPDATE #2: Clarifications and answers to questions

After sifting through the 212 comments posted in the last 12 hours at Anthony Watts’ site, I thought I would answer those concerns that seemed most relevant.

Many of the questions and objections posted there were actually answered by others peoples’ posts — see especially the 2 comments by Jim Clarke at time stamps 18:23:56 & 01:32:40. Clearly, Jim understood what I did, why I did it, and phrased the explanations even better than I could have.

Some readers were left confused since my posting was necessarily greatly simplified; the level of detail for a journal submission would increase by about a factor of ten. I appreciate all the input, which has helped clarify my thinking.

RATIONALE FOR THE STUDY

While it might not have been obvious, I am trying to come up with a quantitative method for correcting past temperature measurements for the localized warming effects due to the urban heat island (UHI) effect. I am generally including in the “UHI effect” any replacement of natural vegetation by manmade surfaces, structures and active sources of heat. I don’t want to argue about terminology, just keep things simple.

For instance, the addition of an outbuilding and a sidewalk next to an otherwise naturally-vegetated thermometer site would be considered UHI-contaminated. (As Roger Pielke, Sr., has repeatedly pointed out, changes in land use, without the addition of manmade surfaces and structures, can also cause temperature changes. I consider this to be a much more difficult influence to correct for in the global thermometer data.)

The UHI effect leads to a spurious warming signal which, even though only local, has been given global significance by some experts. Many of us believe that as much as 50% (or more) of the “global warming” signal in the thermometer data could actually be from local UHI effects. The IPCC community, in contrast, appears to believe that the thermometer record has not been substantially contaminated.

Unless someone quantitatively demonstrates that there is a significant UHI signal in the global thermometer data, the IPCC can claim that global temperature trends are not substantially contaminated by such effects.

If there were sufficient thermometer data scattered around the world that are unaffected by UHI effects, then we could simply throw away all of the contaminated data. A couple of people wondered why this is not done. I believe that there is not enough uncontaminated data to do this, which means we must find some way of correcting for UHI effects that exist in most of the thermometer data — preferably extending back 100 years or more.

Since population data is one of the few pieces of information that we have long term records for, it makes sense to determine if we can quantify the UHI effect based upon population data. My post introduces a simple method for doing that, based upon the analysis of global thermometer and population density data for a single year, 2000. The analysis needs to be done for other years as well, but the high-resolution population density data only extends back to 1990.

Admittedly, if we had good long-term records of some other variable that was more closely related to UHI, then we could use that instead. But the purpose here is not to find the best way to estimate the magnitude of TODAY’S UHI effect, but to find a practical way to correct PAST thermometer data. What I posted was the first step in that direction.

Clearly, satellite surveys of land use change in the last 10 or 20 years are not going to allow you to extend a method back to 1900. Population data, though, ARE available (although of arguable quality). But no method will be perfect, and all possible methods should be investigated.

STATION PAIRING

My goal is to quantify how much of a UHI temperature rise occurs, on average, for any population density, compared to a population density of zero. We can not do this directly because that would require a zero-population temperature measurement near every populated temperature measurement location. So, we must do it in a piecewise fashion.

For every closely-spaced station pair in the world, we can compare the temperature difference between the 2 stations to the population density difference between the two station locations. Using station pairs is easily programmable on a computer, allowing the approx 10,000 temperature measurements sites to be processed relatively quickly.

Using a simple example to introduce the concept, theoretically one could compute:

1) how much average UHI warming occurs from going from 0 to 20 people per sq. km, then
2) the average warming going from 20 to 50 people per sq. km, then
3) the average warming going from 50 to 100 people per. sq. km,
etc.

If you can compute all of these separate statistics, we can determine how the UHI effect varies with population density going from 0 to the highest population densities.

Unfortunately, the populations of any 2 closely-spaced stations will be highly variable, not neatly ordered like this simple example. We need some way of handling the fact that stations do NOT have population densities exactly at 0, 20, 100 (etc.) persons per sq. km., but can have ANY population density. I handle this problem by doing averaging in specific population intervals.

For each pair of closely spaced stations, if the higher-population station is in population interval #3, and the lower population station is in population interval #1, I put that station pair’s year-average temperature difference in a 2-dimensional (interval#3, interval#1) population “bin” for later averaging.

Not only is the average temperature difference computed for all station pairs falling in each population bin, but also computed are the average populations in those bins. We will need those statistics later for our calculations of how temperature increases with population density.

Note that we can even compute the temperature difference between stations in the SAME population bin, as long as we keep track of which one has the higher population and which has the lower population. If the population densities for a pair of stations are exactly the same, we do not include that pair in the averaging.

The fact that the greatest warming RATE is observed at the lowest population densities is not a new finding. My comment that the greatest amount of spurious warming might therefore occur at the rural (rather than urban) sites, as a couple of people pointed out, presumes that rural sites tend to increase in population over the years. This might not be the case for most rural sites.

Also, as some pointed out, the UHI warming will vary with time of day, season, geography, wind conditions, etc. These are all mixed in together in my averages. But the fact that a UHI signal clearly exists without any correction for these other effects means that the global warming over the last 100 years measured using daily max/min temperature data has likely been overestimated. This is an important starting point, and its large-scale, big-picture approach complements the kind of individual-station surveys that Anthony Watts has been performing.